Patient Predictor

Modeling Patient Length of Stay from Hospital Records Data

Vladimir Turzhitsky,  INSIGHT HEALTH DATA SCIENCE FELLOW, BOSTON WINTER 2018

In this project, I consulted a health analytics startup on developing a predictive model for the length of hospital stay from patient data. The data were obtained  from the electronic medical records of a hospital system in the form of several relational tables. The major goals of the consulting project were to

  • Build an accurate predictive model for the length of patient hospital stays. 
  • Easily interpretable models for explanation to hospital administrative staff are preferred
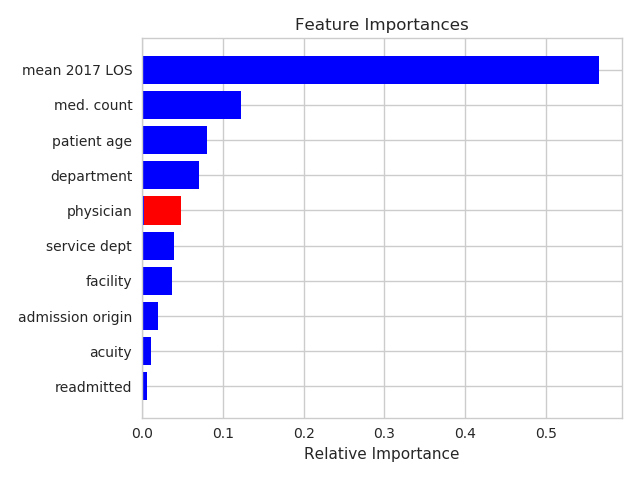
  • The model should allow understanding and quantification of the effect that a physician has on the length of patient hospital stays.

Why Is Knowing Patient Length of Stay (LOS) Important?

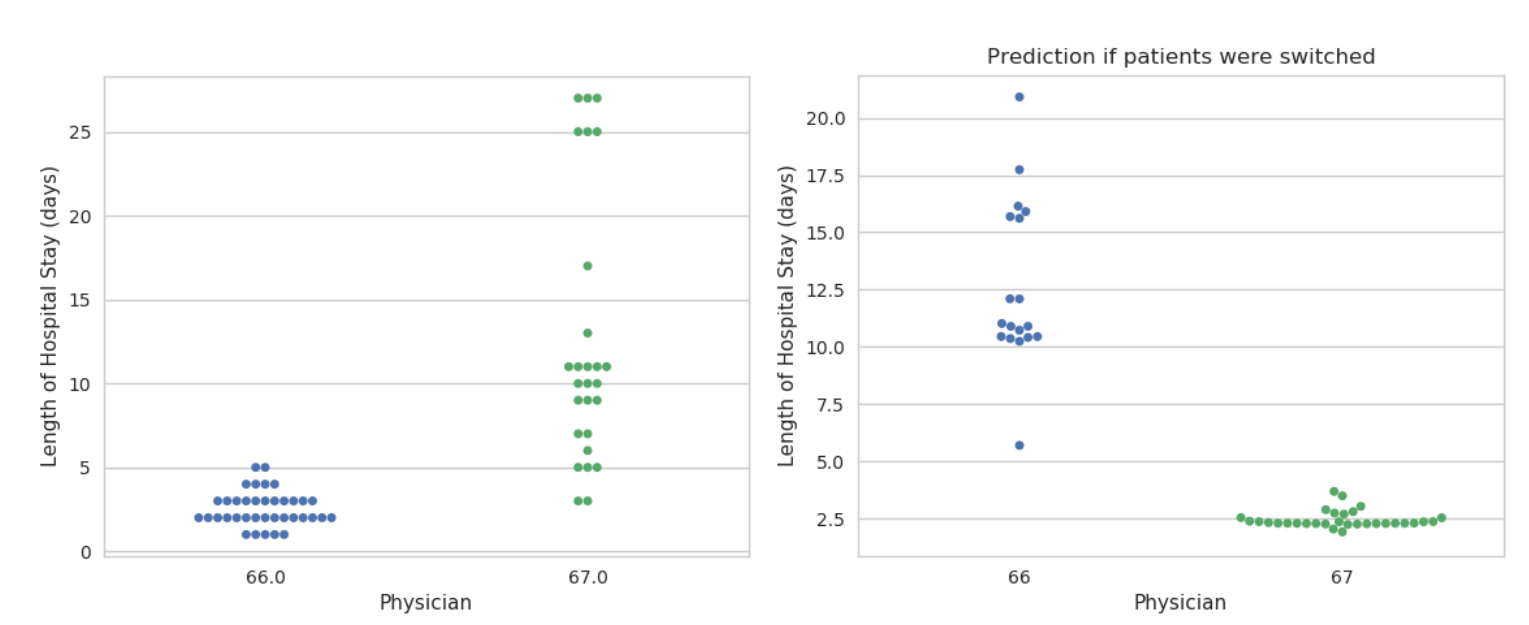
Considering that each patient day in the hospital costs approximately $1,900, and the current reimbursement system only provides a flat dollar amount per patient based on their diagnosis, without regard to the actual time spent, identifying patient costs before they are incurred is the first step toward implementing cost-saving measures. One example is the effectiveness of a particular physician at resulting in a decreased length of stay for patients. 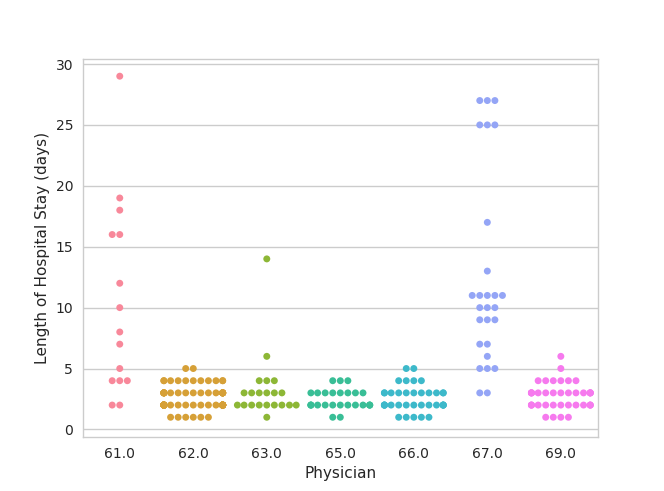In other words, if the patient had a different doctor, would they have gotten discharged faster? For example, if we look at physicians and their patients’ lengths of hospital stays, we can clearly observe that certain physicians have more patients with longer stays (figure 1). However, we also know that patients have widely varying conditions and the length of stay depends on the patient diagnosis in addition the the patient age and other factors that affect complexity. Taking these factors into account can should improve the predictability of the length of stay.

Figure 1. Length of stay observations for individual patient visits grouped by physicians.

Model Variable Choices

Time of prediction

Many of the features that influence the patients length of stay may evolve over the course of the visit and are correlated with the length of the visit. For example, the number of blood tests done and the number of medications given all increase linearly with the length of the visit because patients often have daily blood tests and medication doses. However, for the model to be useful, it is important to select a time point at which the length of stay prediction is done. I chose to predict the length of stay on day 1 of the visit in order to have the biggest opportunity of influencing the outcome. This early time point gives the administration the opportunity of optimizing physician-patient assignments.

Inclusion Criteria

The dataset were obtained from the electronic medical records of a hospital network within the region of the health analytics startup. I restricted my analysis to visits that had sufficient information to obtain the length of stay (admission and discharge dates). I presumed that patients with very long lengths of stay, greater than a month, are there for reasons outside of the scope of their medical care and therefore excluded them from the analysis. I also excluded patients who died during their stay. This resulted in about 40,000 remaining hospital visits. However, when grouping the patients by their type, I observed that only about 12,000 of these were inpatient visits (figure 2). Emergency room, Observation, and Nuclear Medicine visits all had very narrow LOS distribution but accounted for over half of the observations. Surprisingly, outpatient visit LOS values were very widely distributed. After discussing this observation with the company, I learned that these patients likely came from outpatient facilities, such as nursing homes or rehab centers, which are not of interest in this analysis. 

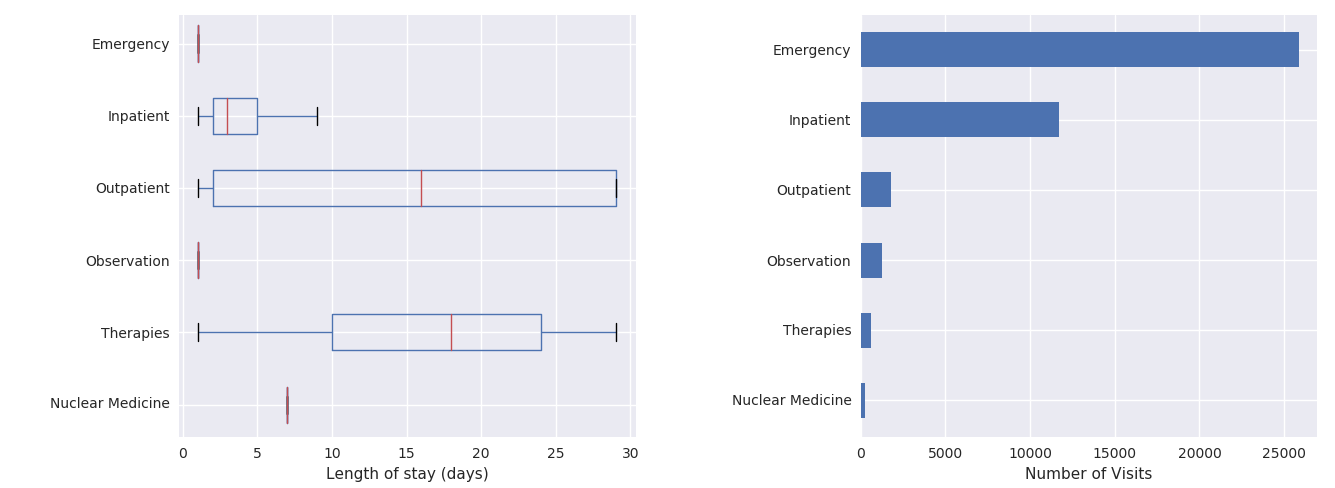
Figure 2. Boxplot of patient categories (left) and corresponding number of observed visits (right).

I proceeded with building a model for exclusively inpatient visits. Note that the boxplots do not show the outliers, which extend all the way out to 30 days, given the long-tailed distribution of hospital stay lengths.

Features & Model

A few preparatory steps were taken to re-package the available information into format amenable for modeling.

  • A table with detailed medication data was used to count the number of medication order types each visit had within the first day. The number of different types of medications would indicated a more complex patient.
  • Physician was taken as the first assigned attending physician for that patient visit.
  • Patient Age was constructed from patient birth date and admission date.
  • Patient Age was constructed from patient birth date and admission date.
    All other available categorical variables were used, including diagnosis, facility, department, whether or not the visit is a readmission, where the patient is admitted from etc. Each of these categorical variables were 1-hot-encoded.
  • All sparse categories with fewer than 50 observations/category were lumped into a single group. Physicians with fewer than 10 patients were also lumped into a single group.

Treatment of Patient Diagnosis

Initially, I built a model using the diagnosis as a categorical predictor of the LOS. There were approximately 200 different diagnoses with a substantial number of observations in the data set. There was also information about the national average LOS that corresponds to each diagnosis category. This national average LOS is used as one of the factors for determining insurance payments to the hospital. I found that models that used the mean national LOS had a higher prediction accuracy than those that include individual diagnosis categories, and therefore used this predictor in place of the diagnosis category. Only about 75% of the patient visits had this value available, which slightly reduced the number of visits in the model.

Baseline Model

As a baseline prediction model, I performed a regression of the observed LOS on the national average LOS for the diagnosis category. This is the predictor which is currently used by most hospital systems and is a reasonable baseline performance metric.

Regularized Ridge Regression Model

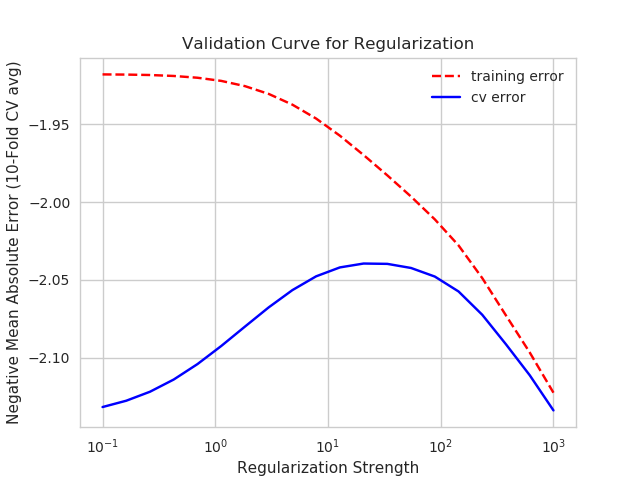
As an initial model, I performed a regularized multivariate linear regression of the LOS on all of the features, including the national mean LOS for the diagnosis. I did this using the Ridge regression from the scikit-learn Python package. I split the data into 80% training/validation and 20% testing. I performed 10-fold cross-validation using an 80/20 training/validation split. This procedure randomly shuffles the training/validation set 10 times and splits the set 80/20 for each shuffling instance. Learning curves showed that the model training and validation performance were very close after training on 5000 visits. The regularization strength was optimized based on the training/validation set and gave a minor improvement (figure 4) because the training/validation errors were already very close.

shaded_lines_linreg

Figure 3. Learning curves for linear regression without regularization. A linear regression using exclusively the the national average LOS for the patient-specific diagnosis is used as a baseline prediction. The solid lines represent the average performance of the validation sets and the shaded region represents +/- one standard deviation.



Figure 4. Optimization of the regularization strength for multivariate linear regression model. Because the training and CV errors are already very close, regularization improves the model performance by less than 5%.

The linear regression model already outperforms the baseline prediction, but it makes several assumptions that may decrease its performance. As mentioned above, it assumes the dependent variable is normally distributed, which is not the case for hospital LOS data. Secondly, it doesn’t take interactions between features into account. To check how much these assumptions affect the performance of the prediction, I decided to try a more flexible model which can accommodate both of these cases: random forest. 

Random Forest Regression Model

I used the same features as described above in the scikit-learn implementation of the random forest regression. Instead of 1-hot encoding the categorical features I used numerical values, allowing for a more informative view of the feature importances. Learning curves for the random forest regression, again compared to the baseline mean national average for the patient-specific diagnosis, is shown in figure 5. The model was optimized with a grid search using 5-fold cross-validation over the maximum tree depth, minimum samples per leaf, and number of trees, with the optimal values being 10, 5, and 1000 respectively. The optimized random forest model showed a substantial improvement over the linear regression, surpassing the baseline model with very few training examples. Although there was a larger gap between the training and validation set errors at the largest training set size, this indicates that the performance could be further improved if the size of the training data is increased. The optimized random forest regression model had an mean absolute error of 1.68 days in the testing set.

shaded_lines

Figure 5. Random forest regression learning curves compared with baseline regression model as above. The validation set outperforms the baseline model by a larger margin than the linear regression model. The model also looks like it could learn more if the number of training examples were increased.




Figure 6. Feature importance for random forest model. As expected, the most important feature is the national mean LOS. The physician importance (red bar) ranked fifth on the list.

Applications of Model

Now that we have a model, we can use it to answer prospective questions such as “if a patient had a different doctor, what would their predicted length of stay be?”. Figure 7 shows a patient from the testing set and plots this patients predicted length of stay for each of the physicians in the data set. Most of the physicians result in a similar LOS, which is around 9 days. There is one physician which for which the patient was predicted to have a substantially longer stay, more than 12 days. The particular reason for this may be of interest when assigning patients to physicians.

Bokeh Plot
Figure 7. Predicted length of stay for a single patient with different physicians.

Another question we can ask is related to figure 1. Figure 1 shows that some physicians have patients that result in longer lengths of stays. What if two physicians could switch patients? How different would their predicted performance be on each others patients? Two of the physicians and their observed patient lengths of stay are shown in figure 8. Figure 8 shows the predicted lengths of stay if the physicians had switched patients.

Figure 8. Observed patient lengths of stay for two selected physicians.

Future Improvements

Based on this analysis, we can gain some intuition about what next steps can be taken to improve the performance of the model. The most obvious would be to include more features that capture the complexity of the patient case. Although I included age and number of medications, there are a few obvious choices that seem important:

  • Patient body mass index (BMI): patients who are obese tend to have more complications.
  • Co-morbidities: other secondary conditions often make patient treatment more complex (e.g. diabetes, heart disease, cancer, etc.)
  • Patient race: physicians may perform better with patients of the same race.
  • Physician experience: does experience correlate with performance?

These are just a few of the important questions that can be addressed with this kind of model. Each of which could influence the decision making process that underlies physician-patient assignment. I expect that incorporating these factors would improve the performance of the model. But, there may be an inherent amount of uncertainty that simply results from uncertainty which is difficult to quantify.